Coursera 기계 학습 특화 과정 Week 1&2

작성자: 정석훈

본 글은 Coursera에서 제공하는 기계 학습 특화 과정의 1주차, 2 내용을 정리한 글입니다.

---

기계 학습(Machine Learning)은 미국의 컴퓨터 과학자 아서 새뮤얼이 보급한 용어로, 그는 기계 학습을 아래와 같이 정의했습니다.

기계 학습이란, 명시적인 프로그래밍 없이 컴퓨터가 학습하는 능력을 부여하고자 하는 학문이다.

대표적인 기계 학습 알고리즘은 지도 학습(Supervised Learning), 비지도 학습(Unsupervised Learning), 추천 시스템(Recommender Systems), 강화 학습(Reinforcement Learning) 등이 있습니다.

지도 학습

지도 학습은 어떠한 입력데 대한 올바른 정답, 소위 “라벨”이 있는 데이터에서 학습하는 방법을 말합니다. 예를 들면. 이메일(입력)-스팸 여부(라벨), 목소리(입력)-받아쓰기(라벨), 영어(입력)-한국어(라벨) 등이 있습니다. 지도 학습은 크게 회귀(Regression)와 분류(Classification) 과제에 사용됩니다. 회귀는 입력받은 데이터를 바탕으로 특정한 수를 예측하는 경우로, 출력값의 종류는 무한합니다. 예를 들어 집의 평수를 입력하면 집의 가격을 출력하는 과제가 있습니다. 분류는 입력받은 데이터를 바탕으로 정해진 분류 중 하나를 선택하는 경우입니다. 예를 들면 환자의 나이와 종양 크기를 입력하면 암 발병 여부를 출력하는 과제가 있습니다.

비지도 학습

비지도 학습은 지도 학습과는 반대로 라벨이 없는 데이터에서 학습하는 방법입니다. 대신 데이터에서 특정한 패턴을 찾아내는 일을 합니다. 비슷한 특성의 데이터들을 그룹으로 묶는 군집화(Clustering)가 비지도 학습에 속합니다. 독자가 뉴스를 읽을 때, 군집화 알고리즘을 통해 관련된 뉴스를 같이 제시하면 독자의 흥미를 더 끌 수 있겠죠? 이런 경우에 비지도 학습을 사용합니다. 이외에도 비정상적인 데이터를 찾아내는 이상치 탐지(Anomaly Detection), 데이터를 압축하는 차원 축소(Dimensionality Reduction)도 비지도 학습에 해당합니다.

선형 회귀(Linear Regression)

선형 회귀는 기본적으로 데이터를 잘 표현하는 직선을 긋는 것으로 생각할 수 있습니다.

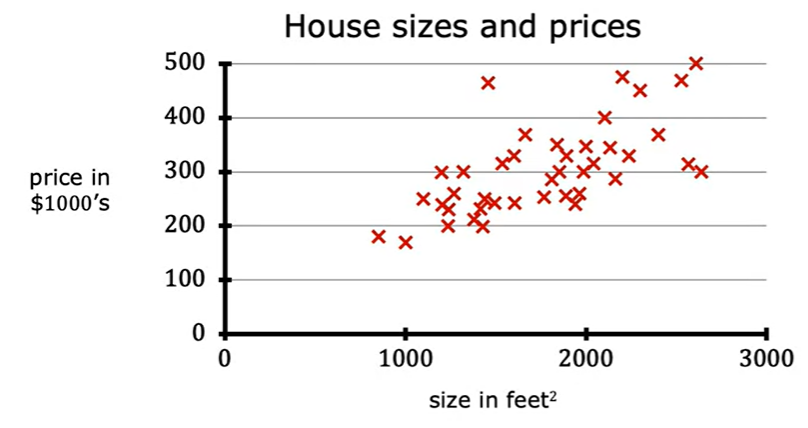
위에서 언급했듯, 회귀는 대표적인 지도 학습입니다. 위 사진처럼 집의 크기(입력)-집의 가격(라벨) 쌍이 데이터로 주어집니다.

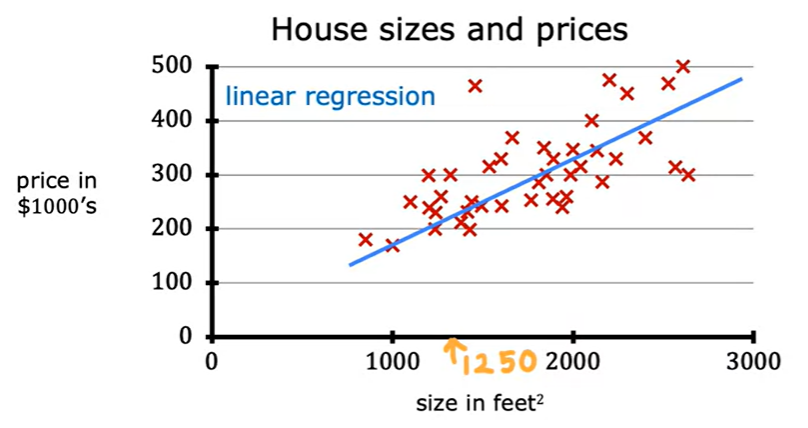
여기에 적당히 직선을 긋는다면, 물론 사람마다 다르겠지만 이 정도로 그을 수 있을 것입니다. 이 직선을 어떻게 잘 그을 것인가가 선형 회귀의 핵심이라고 볼 수 있습니다.

자주 쓰이는 표기법
$x$: 입력 변수
$y$: 출력 변수 / 목표 변수
$m$: 훈련 예시 개수
$(x,y)$: 하나의 훈련 예시
$(x^{(i)},y^{(i)})$: $i$번째 훈련 예시
$\hat{y}$: 훈련시킨 모델이 예측한 값
$f$: 훈련시킨 모델. 선형 회귀에서는 일반적으로 $f_{w,b}(x)=wx+b$로 표현한다.
$w$: 훈련 과정에서 조절되는 매개변수. 계수, 가중치 등으로 불림.
$b$: 훈련 과정에서 조절되는 매개변수. 편향, 절편 등으로 불림. 함수의 위치를 바꾸는 역할을 한다.

손실 함수(Cost Function)

위에서 말한 “직선을 잘 긋는 방법”의 핵심은 손실 함수(또는 비용 함수)입니다. 선형회귀에서의 손실 함수는 아래와 같이 표현됩니다. \(J(w,b) = \dfrac{1}{2m}\sum^m_{i=1}(\hat{y}^{(i)}-y^{(i)})^2\) 이것을 말로 간단하게 풀어 보면, 모델이 예측한 값($\hat{y}$)과 실제 값($y$)의 차이를 손실로 따지는 것입니다. 당연하게도, 우리는 훈련 과정에서 이 차이를 최소화시키고 싶을 것입니다. 손실 함수의 형태를 보면 2차 함수의 모양입니다. 즉, 손실 함수의 최솟값을 찾기 위해, 2차 함수의 최솟값을 찾으면 되는 것입니다.

경사 하강법(Gradient Descent)

손실 함수를 최소화하는 대표적인 알고리즘이 경사하강법입니다. 구체적인 방법은 다음과 같습니다.

1. 특정 $w$, $b$ 값으로 시작한다. 최선은 아니지만 가장 간단한 방법은 $w=0$, $b=0$으로 초기화하는 것.
2. $w$, $b$를 계속 변경해서 $J(w,b)$를 감소시킨다. \(w = w - \alpha \dfrac{\partial}{\partial w}J(w,b)\) \(b = b - \alpha \dfrac{\partial}{\partial b}J(w,b)\)
3. $J(w,b)$가 원하는 만큼 감소할 때까지, 혹은 최소가 될 때까지 2를 반복한다.
   
   

학습률(Learning Rate)

경사 하강법의 2번 단계에서 $\alpha$는 학습률(Learning Rate)로, 한 번에 매개변수를 얼마나 크게 변화시킬지 결정합니다. 높은 학습률과 낮은 학습률에 따른 경사 하강법을 시각화해보면 학습률을 왜 조정해야 하는지 쉽게 알 수 있습니다.

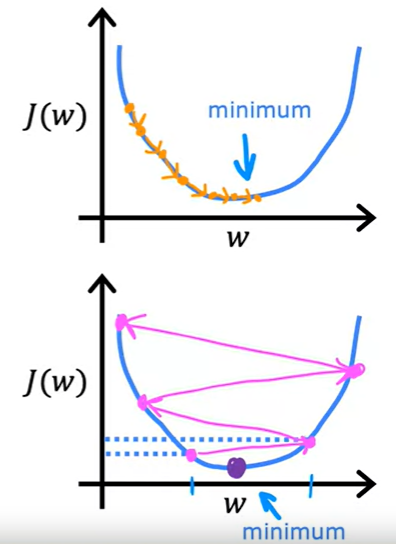
큰 학습률은 매개변수를 크게 변화시키고, 작은 학습률은 매개변수를 조금 변화시킵니다.

선형 회귀에서의 경사 하강법

우리는 선형 회귀의 손실 함수를 이미 정의했습니다. \(J(w,b) = \dfrac{1}{2m}\sum^m_{i=1}(\hat{y}^{(i)}-y^{(i)})^2\) 여기에 경사 하강법을 어떻게 적용하면 될까요? 수식으로 풀어봅시다.

• $w$ 업데이트 \(\dfrac{\partial}{\partial w}J(w,b) = \dfrac{\partial}{\partial w} \dfrac{1}{2m} \sum^m_{i=1} (f_{w,b}(x^{(i)}-y^{(i)})^2\) \(= \dfrac{\partial}{\partial w}\dfrac{1}{2m} \sum^m_{i=1}(wx^{(i)}+b-y^{(i)})^2\) \(= \dfrac{1}{m} \sum^m_{i=1}(wx^{(i)}+b-y^{(i)})x^{(i)}\) \(= \dfrac{1}{m} \sum^m_{i=1}(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)}\)

• $b$ 업데이트 \(\dfrac{\partial}{\partial b}J(w,b) = \dfrac{\partial}{\partial b} \dfrac{1}{2m} \sum^m_{i=1} (f_{w,b}(x^{(i)}-y^{(i)})^2\) \(= \dfrac{\partial}{\partial b}\dfrac{1}{2m} \sum^m_{i=1}(wx^{(i)}+b-y^{(i)})^2\) \(= \dfrac{1}{m} \sum^m_{i=1}(wx^{(i)}+b-y^{(i)})\) \(= \dfrac{1}{m} \sum^m_{i=1}(f_{w,b}(x^{(i)})-y^{(i)})\)
  
  

다중 선형 회귀

지금까지는 하나의 특성(Feature)만을 입력으로 사용하는 단순 선형 회귀를 바탕으로 선형 회귀에 대해 알아보았습니다. 실제로는 둘 이상의 특성을 사용하는 경우가 압도적으로 많을 것입니다. 하지만 지금까지 학습한 내용을 확장하면 다중 선형 회귀에도 쉽게 적용시킬 수 있습니다.
여러 개의 특성을 사용한다는 것은, 예를 들면 집의 가격을 예측하기 위해 집의 크기, 방 수, 층 수, 건설 년도 등의 다양한 정보를 입력받는 것입니다. 여기서 몇 가지 표기법이 추가됩니다.
자주 쓰이는 표기법
$x_j$: $j$번째 특성
$n$: 특성의 개수
$\vec{x}^{(i)}$: $i$번째 훈련 예시의 특성들
$x_j^{(i)}$: $i$번째 훈련 예시의 $j$번째 특성의 값
$f_{\vec{w},b}(x)$: 단순 선형 회귀에서는 $wx+b$였지만, 다중 선형 회귀에서는 $w_1 \cdot x_1+w_2 \cdot x_2+…+w_n \cdot x_n+b$로 표현된다.
$\vec{w}$: 가중치들을 포함하는 벡터

다중 선형 회귀에서의 경사 하강법도 크게 다르지 않습니다. 단순 선형 회귀에서는 $w$와 $b$만 업데이트했다면, 다중 선형 회귀에서는 $w_1,w_2,…,w_n$과 $b$를 업데이트하면 됩니다.

정규 방정식(Normal Equation)

경사 하강법을 사용하지 않고도 $w$와 $b$ 값을 찾는 방법이 있는데요, 바로 정규 방정식입니다. \(W = (X^TX)^{-1}X^Ty\) $W$는 가중치 행렬, $X$는 특성 행렬, $y$는 라벨 벡터입니다. 정규 방정식의 유도는 여기서는 다루지 않겠습니다.
이 방법에는 장단점이 있습니다. 먼저 장점은 반복 업데이트 없이도 $w$와 $b$ 값을 구할 수 있다는 점입니다. 단점으로는 선형 회귀에만 적용이 가능하고, 특성의 개수가 10,000개 이상 급으로 커지면 느리다는 것입니다.

특성 조정(Feature Scaling)

경사 하강법으로 매개변수 값을 찾는 것은 좋은 방법이지만, 이것을 더 효율적으로 만드는 방법이 많습니다. 그 중 대표적인 것이 특성 조정입니다. 다중 선형 회귀에서는 둘 이상의 특성을 사용하게 되는데, 여러 특성들이 항상 일관적인 값을 가지는 것은 아닙니다. 예를 들어, 집의 크기와 방 수라는 특성을 생각해 봅시다. 집의 사이즈는 300ft²에서 2,000ft²까지 있지만, 방 수는 0-5개 정도입니다. 이 경우, 집의 사이즈의 가중치는 매우 작아야 하고, 반대로 방 수의 가중치는 매우 커야 합니다. 가중치가 같은 수치로 주어진다면 집의 사이즈가 총합에 미치는 영향력이 지나치게 클 테니까요.
여기에서 문제가 생깁니다. 경사 하강법으로 가중치를 매우 크게 혹은 매우 작게 변경시키게 될 경우, 우리가 원하는 값으로 수렴하는 데에 더 많은 업데이트가 필요하게 됩니다. 이런 현상을 방지하기 위해 아래와 같은 특성 조정 방법들을 수행합니다.

1. 평균 정규화(Mean Normalization): $x_i = \dfrac{x_i - \mu_i}{max-min}$
2. Z-점수 정규화(Z-score Normalization): $x_i = \dfrac{x_i-\mu_i}{\sigma_i}$
   
   

경사 하강법이 수렴했는가?

특성 조정 등의 방법을 사용해서 결국 우리는 경사 하강법을 통해 손실 함수를 최소화하고 싶습니다. 하지만 과연 경사 하강법을 언제 멈춰야 할까요? 이를 확인하기 위해 학습 곡선(Learning Curve)을 사용합니다. 학습 곡선의 x축은 반복 횟수, y축은 손실 함수의 값입니다.

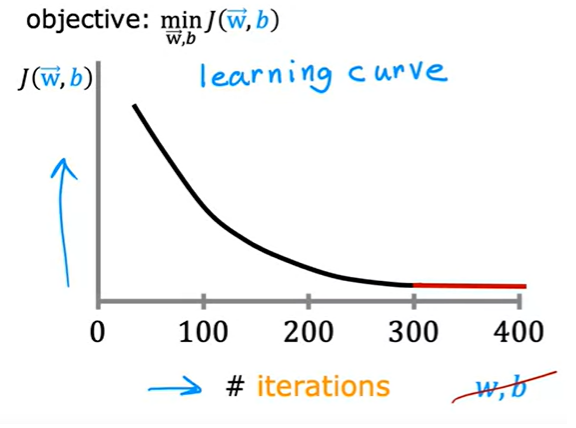
만약 반복 횟수가 늘어도 손실 함수의 값이 줄어들지 않는다면 수렴을 선언할 수 있습니다. 일반적으로 “줄어들지 않는다”의 기준을 어떤 상수 값(예를 들면 $\epsilon = 10^{-3}$)으로 잡고, 그 이하만큼 줄어들면 수렴이라고 칩니다.

학습률을 고르는 방법

여기에서도 역시 학습 곡선을 참고할 수 있습니다. 만약 반복 횟수를 거듭함에도 손실이 증가한다면 학습률이 너무 클 가능성이 있습니다. 반대로 손실 감소가 느리다면, 학습률이 너무 작아서 수렴이 느릴 가능성이 있습니다. 학습률을 고르는 하나의 방법은 다음과 같습니다.
예를 들어, $0.001$이라는 학습률로 시작했다고 가정해 봅시다. 만약 이 값이 너무 작을 경우, 이것을 3배 정도로 키워서 $0.003$을 사용해 봅니다. 그래도 작다면 또 3배 정도를 해서 $0.01$을 사용해 봅니다. 이런 식으로 약 3배 정도씩 곱해서 사용하는 방법이 있습니다. 학습률이 너무 크다면 반대로 1/3배를 하면 되겠죠? 물론 이것은 매우 간단한 방법이고, 좋은 학습률을 선정하는 데에는 많은 방법이 있습니다.

다항 회귀(Polynomial Regression)

지금까지는 직선을 잘 긋고자 하는 선형 회귀 알고리즘에 대해 알아보았습니다. 하지만 세상을 선형적으로만 표현하기에는 한계가 있겠죠? 당연하게도 비선형 데이터를 학습하기 위한 다항 회귀 역시 존재합니다. 이 경우에는 기존의 특성에서 새로운 특성을 만들어내는 특성 공학(Feature Engineering)도 자주 사용됩니다. 예를 들면 길이와 너비라는 특성이 있을 때, 두 값을 곱하여 넓이라는 새로운 특성으로 활용하는 방식이죠. 하지만 현재 단계에서는 자세히 다루지는 않고, Lab 세션에서 scikit-learn을 사용한 알고리즘 사용만 경험해 보도록 하겠습니다.